分类法/范例二: Normal and Shrinkage Linear Discriminant Analysis for classification

http://scikit-learn.org/stable/auto_examples/classification/plot_lda.html

这个范例用来展示scikit-learn 如何使用Linear Discriminant Analysis (LDA) 线性判别分析来达成资料分类的目的

1. 利用 sklearn.datasets.make_blobs 产生测试资料
2. 利用自定义函数 generate_data 产生具有数个特徵之资料集，其中仅有一个特徵对于资料分料判断有意义
3. 使用LinearDiscriminantAnalysis来达成资料判别
4. 比较于LDA演算法中，开启 shrinkage 前后之差异

(一)产生测试资料

从程式码来看，一开始主要为自定义函数generate_data(n_samples, n_features)，这个函数的主要目的为产生一组测试资料，总资料列数为n_samples，每一列共有n_features个特徵。而其中只有第一个特徵得以用来判定资料类别，其他特徵则毫无意义。make_blobs负责产生单一特徵之资料后，利用｀np.random.randn｀　乱数产生其他｀n_features - 1｀个特徵，之后利用np.hstack以"水平" (horizontal)方式连接X以及乱数产生之特徵资料。

%matplotlib inline
from __future__ import division
import numpy as np
import matplotlib.pyplot as plt

from sklearn.datasets import make_blobs
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis

n_train = 20  # samples for training
n_test = 200  # samples for testing
n_averages = 50  # how often to repeat classification
n_features_max = 75  # maximum number of features
step = 4  # step size for the calculation

def generate_data(n_samples, n_features):
    X, y = make_blobs(n_samples=n_samples, n_features=1, centers=[[-2], [2]])
    # add non-discriminative features
    if n_features > 1:
        X = np.hstack([X, np.random.randn(n_samples, n_features - 1)])
    return X, y

我们可以用以下的程式码来测试自定义函式，结果回传了X (10x5矩阵)及y(10个元素之向量)，我们可以使用pandas.DataFrame套件来观察资料

X, y = generate_data(10, 5)

import pandas as pd
pd.set_option('precision',2)
df=pd.DataFrame(np.hstack([y.reshape(10,1),X]))
df.columns = ['y', 'X0', 'X1', 'X2', 'X2', 'X4']
print(df)

结果显示如下。。我们可以看到只有X的第一行特徵资料(X0) 与目标数值 y 有一个明确的对应关系，也就是y为1时，数值较大。

       y    X0    X1    X2    X2    X4
    0  1  0.38  0.35  0.80 -0.97 -0.68
    1  1  2.41  0.31 -1.47  0.10 -1.39
    2  1  1.65 -0.99 -0.12 -0.38  0.18
    3  0 -4.86  0.14 -0.80  1.13 -1.31
    4  1 -0.06 -1.99 -0.70 -1.26 -1.64
    5  0 -1.51 -1.74 -0.83  0.74 -2.07
    6  0 -2.50  0.44 -0.45 -0.55 -0.42
    7  1  1.55  1.38  0.93 -1.44  0.27
    8  0 -1.95  0.32 -0.28  0.02  0.07
    9  0 -0.58 -0.07 -1.01  0.15 -1.84

(二)改变特徵数量并测试shrinkage之功能

接下来程式码里有两段迴圈，外圈改变特徵数量。内圈则多次尝试LDA之以求精准度。使用LinearDiscriminantAnalysis来训练分类器，过程中以shrinkage='auto'以及shrinkage=None来控制shrinkage之开关，将分类器分别以clf1以及clf2储存。之后再产生新的测试资料将准确度加入score_clf1及score_clf2里，离开内迴圈之后除以总数以求平均。

acc_clf1, acc_clf2 = [], []
n_features_range = range(1, n_features_max + 1, step)
for n_features in n_features_range:
    score_clf1, score_clf2 = 0, 0
    for _ in range(n_averages):
        X, y = generate_data(n_train, n_features)

        clf1 = LinearDiscriminantAnalysis(solver='lsqr', shrinkage='auto').fit(X, y)
        clf2 = LinearDiscriminantAnalysis(solver='lsqr', shrinkage=None).fit(X, y)

        X, y = generate_data(n_test, n_features)
        score_clf1 += clf1.score(X, y)
        score_clf2 += clf2.score(X, y)

    acc_clf1.append(score_clf1 / n_averages)
    acc_clf2.append(score_clf2 / n_averages)

(三)显示LDA判别结果

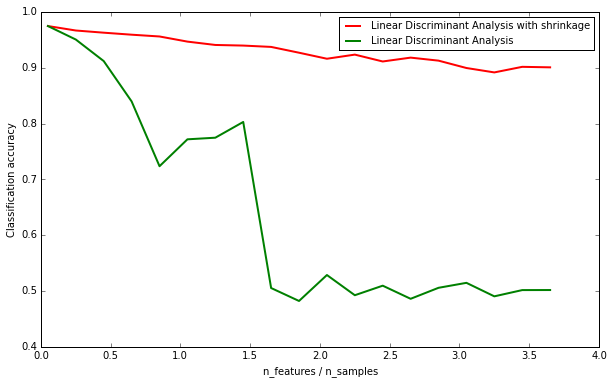
这个范例主要希望能得知shrinkage的功能，因此画出两条分类准确度的曲线。纵轴代表平均的分类准确度，而横轴代表的是features_samples_ratio 顾名思义，它是模拟资料中，特徵数量与训练资料列数的比例。当特徵数量为75且训练资料列数仅有20笔时，features_samples_ratio = 3.75 由于资料列数过少，导致准确率下降。而此时shrinkage演算法能有效维持LDA演算法的准确度。

features_samples_ratio = np.array(n_features_range) / n_train
fig = plt.figure(figsize=(10,6), dpi=300)
plt.plot(features_samples_ratio, acc_clf1, linewidth=2,
         label="Linear Discriminant Analysis with shrinkage", color='r')
plt.plot(features_samples_ratio, acc_clf2, linewidth=2,
         label="Linear Discriminant Analysis", color='g')
plt.xlabel('n_features / n_samples')
plt.ylabel('Classification accuracy')

plt.legend(loc=1, prop={'size': 10})
plt.show()

(四)完整程式码

Python source code: plot_lda.py

from __future__ import division

import numpy as np
import matplotlib.pyplot as plt

from sklearn.datasets import make_blobs
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis


n_train = 20  # samples for training
n_test = 200  # samples for testing
n_averages = 50  # how often to repeat classification
n_features_max = 75  # maximum number of features
step = 4  # step size for the calculation


def generate_data(n_samples, n_features):
    """Generate random blob-ish data with noisy features.

    This returns an array of input data with shape `(n_samples, n_features)`
    and an array of `n_samples` target labels.

    Only one feature contains discriminative information, the other features
    contain only noise.
    """
    X, y = make_blobs(n_samples=n_samples, n_features=1, centers=[[-2], [2]])

    # add non-discriminative features
    if n_features > 1:
        X = np.hstack([X, np.random.randn(n_samples, n_features - 1)])
    return X, y

acc_clf1, acc_clf2 = [], []
n_features_range = range(1, n_features_max + 1, step)
for n_features in n_features_range:
    score_clf1, score_clf2 = 0, 0
    for _ in range(n_averages):
        X, y = generate_data(n_train, n_features)

        clf1 = LinearDiscriminantAnalysis(solver='lsqr', shrinkage='auto').fit(X, y)
        clf2 = LinearDiscriminantAnalysis(solver='lsqr', shrinkage=None).fit(X, y)

        X, y = generate_data(n_test, n_features)
        score_clf1 += clf1.score(X, y)
        score_clf2 += clf2.score(X, y)

    acc_clf1.append(score_clf1 / n_averages)
    acc_clf2.append(score_clf2 / n_averages)

features_samples_ratio = np.array(n_features_range) / n_train

plt.plot(features_samples_ratio, acc_clf1, linewidth=2,
         label="Linear Discriminant Analysis with shrinkage", color='r')
plt.plot(features_samples_ratio, acc_clf2, linewidth=2,
         label="Linear Discriminant Analysis", color='g')

plt.xlabel('n_features / n_samples')
plt.ylabel('Classification accuracy')

plt.legend(loc=1, prop={'size': 12})
plt.suptitle('Linear Discriminant Analysis vs. \
shrinkage Linear Discriminant Analysis (1 discriminative feature)')
plt.show()