线性回归分析: Property value prediction
此档案使用scikit-learn 机器学习套件裡的linear regression演算法,来达成波士顿房地产价钱预测
- 资料集:波士顿房产
- 特徵:房地产客观数据,如年份、平面大小
- 预测目标:房地产价格
- 机器学习方法:线性迴归
- 探讨重点:10 等分的交叉验証(10-fold Cross-Validation)来实际测试资料以及预测值的关系
- 关键函式:
sklearn.cross_validation.cross_val_predict;joblib.dump;joblib.load
(一)引入函式库及内建波士顿房地产资料库
引入之函式库如下
sklearn.datasets: 用来汇入内建之波士顿房地产资料库sklearn.cross_val_predict: 使用交叉验证用来评估辨识准确度sklearn.linear_model: 线性分析之模组matplotlib.pyplot: 用来绘製影像
from sklearn import datasets
from sklearn.cross_validation import cross_val_predict
from sklearn import linear_model
import matplotlib.pyplot as plt
lr = linear_model.LinearRegression()
# The boston dataset
boston = datasets.load_boston()
y = boston.target
使用linear_model.LinearRegression()将线性迴归分析演算法引入到lr。
使用datasets.target将士顿房地产资料的预测数值汇入到y。
使用 datasets.load_boston() 将资料存入, boston 为一个dict型别资料,我们看一下资料的内容。
| 显示 | 说明 |
|---|---|
| ('data', (506, 13)) | 房地产的资料集,共506笔房产13个特徵 |
| ('feature_names', (13,)) | 房地产的特徵名 |
| ('target', (506,)) | 回归目标 |
| DESCR | 资料之描述 |
(二)cross_val_predict的使用
sklearn.cross_validation.cross_val_predict(estimator, X, y=None, cv=None, n_jobs=1, verbose=0, fit_params=None, pre_dispatch='2*n_jobs')
X为机器学习数据, y为回归目标, cv为交叉验証时资料切分的依据,范例为10则将资料切分为10等分,以其中9等分为训练集,另外一等分则为测试集。
predicted = cross_val_predict(lr, boston.data, y, cv=10)
(三)使用joblib.dump汇出预测器
from sklearn.externals import joblib
joblib.dump(lr,"./lr_machine.pkl")
使用joblib.dump将线性回归预测器汇出为pkl档。
(四)训练以及分类
接著使用lr=joblib.load("./lr_machine.pkl")将pkl档汇入为一个linear regression预测器lr。接著使用波士顿房地产数据(boston.data),以及预测目标(y)来训练预测机lr lr.fit(boston.data, y)。最后,使用predict_y=lr.predict(boston.data[2])预测第三笔资料的价格,并将结果存入predicted_y变数。
lr=joblib.load("./lr_machine.pkl")
lr.fit(boston.data, y)
predict_y=lr.predict(boston.data[2])
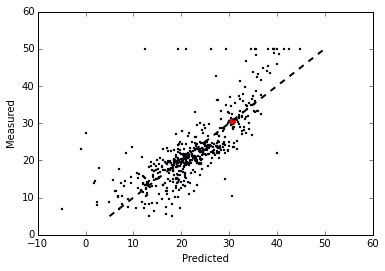
(五)绘出预测结果与实际目标差异图
X轴为预测结果,Y轴为回归目标。 并划出一条斜率=1的理想曲线(用虚线标示)。
红点为房地产第三项数据的预测结果。
plt.scatter(predicted,y,s=2)
plt.plot(predict_y, predict_y, 'ro')
plt.plot([y.min(), y.max()], [y.min(), y.max()], 'k--', lw=2)
plt.xlabel('Predicted')
plt.ylabel('Measured')
(六)完整程式码
%matplotlib inline
from sklearn import datasets
from sklearn.cross_validation import cross_val_predict
from sklearn import linear_model
import matplotlib.pyplot as plt
lr = linear_model.LinearRegression()
boston = datasets.load_boston()
y = boston.target
# cross_val_predict returns an array of the same size as `y` where each entry
# is a prediction obtained by cross validated:
predicted = cross_val_predict(lr, boston.data, y, cv=10)
from sklearn.externals import joblib
joblib.dump(lr,"./lr_machine.pkl")
lr=joblib.load("./lr_machine.pkl")
lr.fit(boston.data, y)
predict_y=lr.predict(boston.data[2])
plt.scatter(predicted,y,s=2)
plt.plot(predict_y, predict_y, 'ro')
plt.plot([y.min(), y.max()], [y.min(), y.max()], 'k--', lw=2)
plt.xlabel('Predicted')
plt.ylabel('Measured')